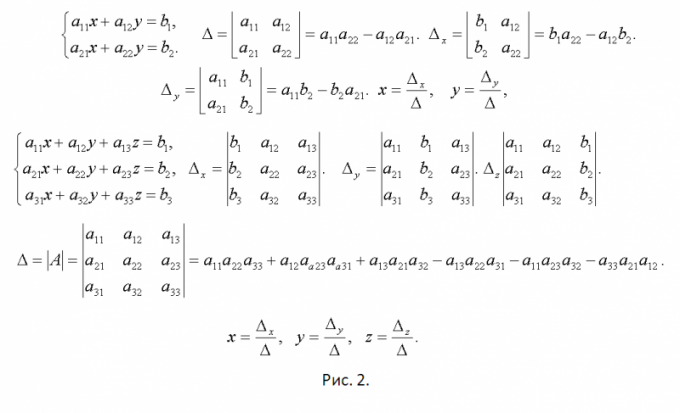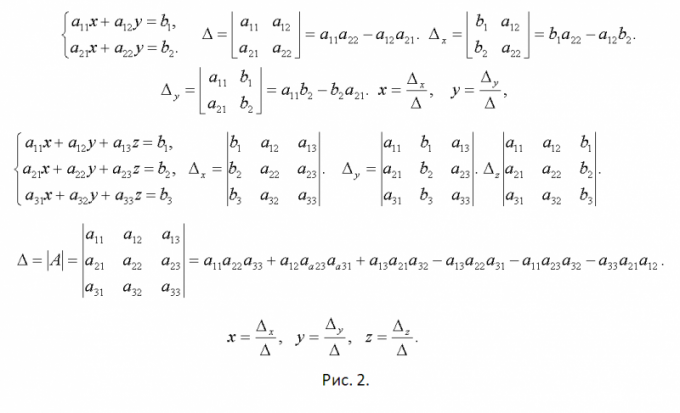LovesTheTeam.com

Metoda supstitucije

Razumjeti bit ove metode je najlakšeprimjer rješenja jedne od tipičnih sustava, koja uključuje dvije jednadžbe i zahtijeva pronalaženje vrijednosti dvaju nepoznanica. Dakle, u ovom svojstvu, može djelovati sljedeći sustav, koji se sastoji od jednadžbi x + 2y = 6 i x - 3y = -18. Da bi se riješio metodom supstitucije, potrebno je u bilo kojoj od jednadžbi izraziti jedan termin preko drugog. Na primjer, to se može učiniti pomoću prve jednadžbe: x = 6 - 2y. Zatim je potrebno zamijeniti dobiveni izraz u drugoj jednadžbi za x. Rezultat ove zamjene bit će jednakost oblika 6 - 2y - 3y = -18. Izvođenje jednostavnih aritmetičkih proračuna, ova se jednadžba može lako reducirati na standardni oblik 5y = 24, pri čemu y = 4,8. Nakon toga, dobivena vrijednost treba biti zamijenjena izrazu koji se koristi za supstituciju. Dakle, x = 6 - 2 * 4.8 = -3.6. Potrebno je potvrditi dobivene rezultate tako da ih zamjenjuju u obje jednadžbe izvornog sustava. To daje sljedeće jednake: -3,6 + 2 * 4,8 = 6 i -3,6 - 3 * 4,8 = -18. Oba su jednaka ispravna pa možemo zaključiti da je sustav ispravno riješen.

Metoda dodavanja

Drugi način rješavanja takvih sustava jednadžbiTo se naziva metodom dodavanja koja se može ilustrirati na temelju istog primjera. Da bi ga koristili, svi članovi jedne od jednadžbi trebaju se pomnožiti određenim koeficijentom, zbog čega jedan od njih postaje suprotno od druge. Izbor ovog koeficijenta provodi se metodom odabira, a isti sustav se može ispravno riješiti različitim koeficijentima. U ovom slučaju, svrhovito je pomnožiti drugu jednadžbu faktorom -1. Tako, prvi jednadžba zadržava svoj izvorni oblik x + 2y = 6, a drugi ima oblik -x + 3y = 18. Potom je potrebno puta dobivene jednadžbe: x + 2y - x + 3y = 6 + 18 Izvođenje jednostavne izračune, moguće je da bi se dobio jednadžba oblika 5y = 24, koja je analogna jednadžbi koja je rezultat otopine sustava metodom supstitucije. Prema tome, korijeni takve jednadžbe također će biti ista vrijednost: x = -3,6, y = 4,8. To jasno pokazuje da su obje metode jednako primjenjive za rješavanje takvih sustava i obje daju iste ispravne rezultate. Izbor metode ovisi o osobnim sklonostima učenika ili određenom izrazu, u kojoj jedan član je lakše izraziti kroz drugu ili odabrati faktor koji će članove dvije jednadžbe suprotno.