LovesTheTeam.com

instrukcija

1

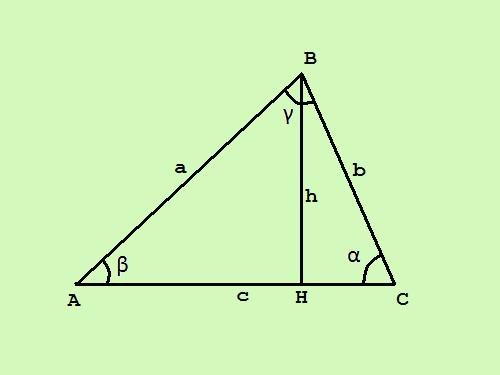
Osnovna formula za područje proizvoljnog trokut ABC se izračunava na sljedeći način: S =? * C * h, gdje je c baza trokut, h je visina privučena ovoj bazi.

2

Formula za izračunavanje područja kroz proizvod strane i kut grijeha između njih je: S = A * b * grijeh.

3

Dopustite krug polumjera r upisivanjem u trokut, a zatim formulu područja trokut će imati oblik: S =? * P * r, gdje P je obod trokut, tj S = A * (A + b + c) * r.

4

Pustite trokut Opisan je krug radijusa R. Oblik područja trokut Kroz polumjer ograničenog kruga i duljinu stranica trokut: S = (a * b * c) / (4 * R). Formula površine trokut Kroz polumjer ograničenog kruga i kutova trokut: S = 2 * R ^ 2 * grijeh * Grijeh * Grijeh?

5

Za četvrt postoji formula Heron trokut, nazvana po starohrvatskom matematičaru Heronu iz Aleksandrije, koji je živio na samom početku naše ere. Ova formula daje definiciju područja kroz duljinu svih strana trokut?: S = * v ((a + b + c) + (b + c - a) * (a + c - b) + (a + b - c)) Snimanje formule uvođenjem semiperimeter pojmova pojednostavljenim :. S = v (p * (p-a) * (p-b) * (p-c)) gdje je p = (a + b + c) / 2 semiperimetar.

6

Formula površine trokut kroz duljinu bočne strane i kutove trokut: S = a ^ 2 * sin? * Grijeh / (2 * sin?), Gdje? i? - susjedni uglovi, eh? - Nasuprot kutu na stranu a.

7

Za pravokutni trokut područje formule je pojednostavljeno i izgleda ovako: S =? * a * b, tj. područje pravokutan trokut je jednak polovici proizvoda duljine nogu.

8

Formula površine za jednakostraničnu trokut: S = (a ^ 2 * v3) / 4.

9

Oblik područja za jednodijelnu pravokutnu oblast trokut: S =? * (A ^ 2 + b ^ 2), gdje a i b su noge trokutOsim toga, za bilo koji trokut Sljedeća nejednakost drži: S <* * (a ^ 2 + b ^ 2).

instrukcija

1

Ako su duljine nogu (a i b) pravokutnogtrokut je izričito naveden pod uvjetima problema, formula za izračunavanje područja (S) ove figure bit će vrlo jednostavna - pomnožite ove dvije veličine i podijelite rezultat na pola: S = ½ * a * b. Na primjer, ako duljine dvije kratke strane takvog trokuta iznose 30 cm i 50 cm, njezino područje treba biti ½ * 30 * 50 = 750 cm2.

2

Ako je trokut postavljen u dvodimenzionalniortogonalni koordinatni sustav i dati koordinate svojih vrhova A (X1, Y1), B (X2, Y2) i C (X3, Y3), počinju izračunavanjem duljine samih nogu. Da biste to učinili, razmotrite trokuta koji se sastoje od svake strane i dvije izbočine na koordinate osi. Činjenica da su ove osi okomite, moguće je pronaći dužinu bočne strane pomoću Pitagoranskog teorema, budući da je to hipoteza u takvom pomoćnom trokutu. Duljine bočnih projekcija (noge pomoćnog trokuta) nalaze se oduzimanjem odgovarajućih koordinata točaka koje tvore stranu. Duljine stranice moraju biti jednake AB | = √ ((X1-X2) ² + (Y1-Y2) ²), | B | = √ ((X2-X3) ² + (Y2-Y3) 2), | CA | = √ ((X3-X1) ² + (Y3-Y1) ²).

3

Odredite koji par stranica su noge- to se može učiniti iz duljina dobivenih u prethodnom koraku. Kathet moraju biti kraći od hipotenusa. Zatim upotrijebite formulu iz prvog koraka - pronađite pola proizvoda izračunatih vrijednosti. Pod uvjetom da su noge AB i BC, opća formula može se napisati na sljedeći način: S = ½ * (√ ((X1-X2) ² + (Y1-Y2) ²) * √ ((X2-X3) (Y2-Y3) 2).

4

Ako je postavljen pravokutni trokuttrodimenzionalni koordinatni sustav, slijed postupaka neće se mijenjati. Jednostavno dodajte formulu za izračunavanje duljine od strane trećih koordinate odgovarajućih točaka: | AB | = √ ((Xi-X₂) ² + (Y₁-Y₂) ² + (Z₁-Z₂) ²), | BUsing | = √ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²), | CA | = √ ((X₃-Xi) ² + (Y₃-Y₁) ² + (Z₃-Z₁) ²). Konačna formula u tom slučaju treba izgledati: S = ½ * (√ ((Xi-X₂) ² + (Y₁-Y₂) ² + (Z₁-Z₂) ²) + √ ((X₂-X₃) ² + (Y₂- Y3) 2 (Z2-Z3) 2).

Trebat će vam

• - Bilježnica;
• - vladar;
• - olovku;
• - ručka;
• - kalkulator.

instrukcija

1

Pravokutnik je četverostrana s ravnim uglovima. Poseban slučaj pravokutnik je trg.područje pravokutnik Je li količina jednaka proizvodu svoje duljine i širine. I kvadrat trga jednak je njezinoj duljini, podignut na drugi stupanj. Ako je samo širina, prvo morate pronaći duljinu, a zatim izračunati područje.

2

Na primjer, s obzirom na pravokutnik ABCD (slika 1), gdje AB = 5 cm, BO = 6,5 cm. Pronađite područje pravokutnik AVCD.

3

jer ABCD - pravokutnik, AO = OS, BO = OD (kao dijagonalne pravokutnik). Razmislite o trokutu ABC. AB = 5 (po konvenciji), AC = 2AO = 13 cm, kut ABC = 90 (budući da je ABCD pravokutnik). Dakle, ABC je pravokutni trokut u kojem su AB i BC katodi, a AC je hipotenuzus (jer je suprotan od pravog kuta).

4

Pythagoreanski teorem kaže: kvadrat hipotenuze jednak je zbroju kvadrata nogu. Po pitagoranskom teoremu pronađite kateter BCBC2 = AC ^ 2 - AB2BBC2 = 13 ^ 2 - 5 ^ 2BC ^ 2 = 169 - 25BC2 = 144BC = √144BC = 12

5

Sada možete pronaći područje pravokutnik ABCD.S = AB * BCS = 12 * 5S = 60.

6

Također je moguće i varijanta širina bit će poznat dijelom. Na primjer, s obzirom na pravokutnik ABCD, gdje AB = 1 / 4AD, OM - medijan trokuta AOD, OM = 3, AO = 5. Pronađite područje pravokutnik AVCD.

7

Razmislite o trokutu AOD. Kut OAD jednak je kutu ODA (jer su AU i BD dijagonalni pravokutnik). Prema tome, trokut A0D je jednoznačan. I u jednodijelnom trokutu, medijan OM je istodobno bisectrix i visina. Stoga je trokut AOM pravokutan.

8

U trokutu AOM, gdje OM i AM su noge, pronađite što je jednako OM (hipotenuzu). Po pitagoranskom teoremu, AM ^ 2 = AO2 - OM2AM = 25-9AM = 16AM = 4

9

Sada izračunajte područje pravokutnik AVCD. AM = 1 / 2AD (jer OM, medijan, dijeli AD na pola). Dakle, AD = 8.AB = 1 / 4AD (po pretpostavci). Stoga AB = 2.S = AB * ADS = 2 * 8S = 16