Savjet 1: Kako dokazati da je trokut pravokutan
Savjet 1: Kako dokazati da je trokut pravokutan
Među mnogim različitim oblicima na ravnini su poligoni. Riječ "poligon" sama označava da postoje drugi kutovi na ovoj slici. trokut je geometrijska slika omeđena s tri međusobno križajuće linije koje tvore tri unutarnje kutove.
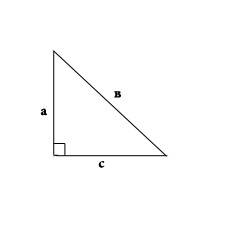
instrukcija
1
Postoje različiti trokuti, na primjer: tup trokut (kut slike veća od 90 stupnjeva), akutne-kut (kut manji od 90 stupnjeva), pravokutnog trokuta (jedan kut trokuta je točno 90 stupnjeva) .Rassmotrim angled trokut i njegova svojstva, koja su postavljena pomoću teorem zbroj kuteva trokuta. Teorem: zbroj dvaju akutnih kutova pravokutnog trokuta je 90 stupnjeva. Zbroj svih kutova u trokutu je 180 stupnjeva, a pravokutni kut je uvijek 90 stupnjeva. Dakle, zbroj dvaju oštrih kutova pravokutnog trokuta je 90 stupnjeva.
2
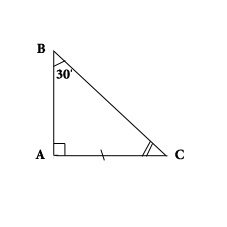
Drugi teorem: katet pravokutnog trokuta nasuprot kutu od 30 stupnjeva je jednak polovici hipotenuse. Razmislite o trokutu ABC. Kut A će biti ravni, kut B 30 stupnjeva, pa je kut C 60 stupnjeva. Potrebno je dokazati da je AC jednak jedan drugi prije Krista. Potrebno je primijeniti trokut ABD na trokut ABC. Dobiva se trokut BHD, u kojem je kut B jednak kutu D, stoga je jednak 60 stupnjeva, tako da je DS BC. Ali AC je jednak jedan drugi DS. Iz toga slijedi da je AC jednak jedan drugi BC.
3
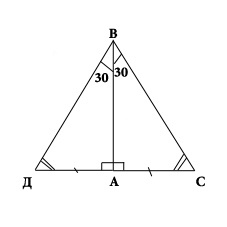
Ako je katet pravokutnog trokuta jednakpola hipotenuze, onda je kut nasuprot nozi je 30 stupnjeva - to je treći teorema.Neobhodimo razmotriti trokuta ABC, čija je noga AC jednaka polovici sunca (hipotenuze). Dajmo dokazati da ABC kut iznosi 30 stupnjeva. Pričvrstite trokut ABD na trokut ABC. Trebao bi biti jednakostraničan trokut VSD (ВС = СД =ДВ). Kutovi takvog trokuta bit će jednaki jedan prema drugom, tako da svaki kut iznosi 60 stupnjeva. Konkretno, kut motora s unutarnjim izgaranjem je 60 stupnjeva, a kut motora s unutarnjim sagorijevanjem jednak je dvama kutovima ABC. Prema tome, kut ABC je 30 stupnjeva. Kao što je potrebno za dokazivanje.

Savjet 2: Kako dokazati da su trokuti jednaki
Dva trokuta su jednaka ako su svi elementi istogsu jednaki elementima druge. Ali nije potrebno poznavati sve dimenzije trokuta kako bi zaključili da su ravnopravni. Dovoljno je imati određene skupove parametara zadanih brojeva.

instrukcija
1
Ako je poznato da dvije strane istetrokut su jednaki dvije strane još i jednakim kutovima između tih strana, trokuta se smatraju jednako. Za dokaz, kombinirajte vrhove jednakih kutova dviju slika. Nastavi sloja. Od rezultirajući zajednički za dva trokuta ukazati poslati jednu stranu kuta trokuta preklapaju na odgovarajućoj strani donjeg slici. Konvencijom, te strane u dva trokuta su jednake. Stoga se krajevi segmenata podudaraju. Stoga je kombiniran drugi par vrhova u danim trokutima. Upute na drugoj strani kuta od kojeg se pokreće dokaz, podudarat će se zbog ravnopravnosti tih kutova. A budući da su te strane jednake, posljednji će se vrh preklapati. Između dvije točke moguće je držati jednu ravnu liniju. Slijedom toga, treće strane u dva trokuta podudaraju se. Dobili ste dva potpuno podudarna broja i dokazani prvi znak jednakosti trokuta.
2
Ako je strana i susjedna dva kuta u jednojtrokut su jednaki odgovarajućim elementima u drugom trokutu, tada su ta dva trokuta jednaka. Da bi se dokazala točnost ove izjave, stavite dvije figure, kombinirajući vrhove jednakih kutova s jednakim stranama. Zbog jednakosti kutova, smjer druge i treće strane će se podudarati, a mjesto njihovog križanja biti će jedinstveno određeno, tj. Treći vrh prvog trokuta nužno se podudara s analognom točkom drugog. Potvrđuje se drugi kriterij za jednakost trokuta.
3
Ako su tri strane jednog trokutaodnosno, jednaki su tri strane druge, tada su ti trokuti jednaki. Poravnajte dva vrha i njihovu stranu tako da jedna figura bude iznad drugih. Postavite kružnu iglu u jedan od zajedničkih vrhova, izmjerite drugu stranu donjeg trokuta i izvucite taj polumjer na gornju polovicu sastava dvaju trokuta. Sada ponovite postupak s drugog uspravljenog vrha s radijusom jednakim trećoj strani. Napravite usjek na raskrižju s prvim lukom. Točka križanja ovih krivulja je samo jedna, i podudara se s trećim vrhom gornjeg trokuta. Pokazali ste izjavu koja se u geometriji zove treći znak jednakosti trokuta.







